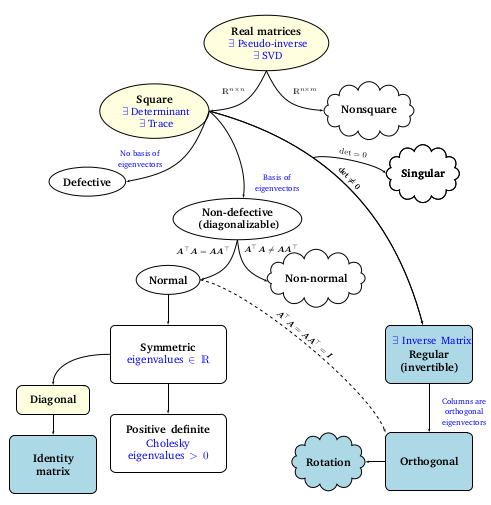
Matrix Decompositions

Trace of a matrix

It’s the sum of diagonal elements of a matrix and is the only function satisfying these 4 properties :

• $\text{tr}(\bold{A+B}) = \text{tr}(\bold{A}) + \text{tr}(\bold{B})$

• $\text{tr}(a\bold{A}) = a\,\text{tr}(\bold{A})$

• $\text{tr}(\bold{I}_n)=n$

• $\text{tr}(\bold{AB}) = \text{tr}(\bold{BA})$

Using the last property, we can get $\text{tr}(\bold{R^{-1}AR}) = \text{tr}(\bold{A})$ , which means that similar matrices have the same trace, and thus for any linear map $f:V\to V$, no matter in what bases it’s expressed, as long as it has same bases on either side, (before the map and after the map), we get the same trace for the matrix representing the map.

Eigenspace and geometric multiplicity of eigenvalues

For a matrix $\bold{A}$ , the Eigenspace of the eigenvalue $\lambda$ , denoted by $E_{\lambda}$ is the null space of $\bold{A-\lambda I}$ .

The geometric multiplicity is the dimension of this null space and the algebraic multiplicity is the number of times this eigenvalue repeats in the roots of characteristic polynomial.

Eigenvalue properties

• A matrix $\bold{A}$ and its transpose $\bold{A}^T$ have the same eigenvalues (not the same eighenvectors) .

• Any linear map always has the same eigevalues, no matter how it is expressed , because the diagonal matrix in the decomposition stays the same (upto rearrangement)

• The sum of eigenvalues is just the trace and the product is the determinant (due to the characteristic polynomial) .

• Eigenvectors with different eigenvalues are linearly independent. Proof by induction : Suppose that this statement is true for $k$ eigenvectors, then consider any $k+1$ eigenvectors with distinct eigenvalues. Assume they are linearly independent, then we can write $0 = a_1\bold{v_1} + a_2\bold{v_2} + \dots a_k\bold{v_k} + a_{k+1}\bold{v_{k+1}}$ where at least 2 of the coefficients must be non zero. Applying the matrix on both sides, we get $0 = a_1\lambda_1\bold{v_1} + \dots a_k\lambda_k\bold{v_k} + a_{k+1}\lambda_{k+1}\bold{v_{k+1}}$. Now subtracting $\lambda_{k+1}$ times the first equation from this, we get : $0 = a_1(\lambda_1-\lambda_{k+1})\bold{v_1} + \dots a_k(\lambda_k-\lambda_{k+1})\bold{v_k}$ , which is basically screaming that $k$ eigenvectors are linearly dependent since not all of the coefficients are $0$ , which is a contradiction. And thus, we have extended the hypothesis to $k+1$ eigenvectors. The base case is for 2 eigenvectors and is trivially true.

Positive definite matrices

Any matrix $\bold{A}$ such that $\bold{x^TAx}>0\;\; \forall \;\bold{x}\in V-\{0\}$ where $V$ is a vector space is positive definite.

Positive definite matrices always have positive eigenvalues if they are real, since for any such matrix $\bold{A}$ with any eigenvector $\bold{v}$ with eigenvalue $\lambda$ , we have $\bold{v^TAv} >0 \implies \bold{v^T\lambda v} = \lambda ||\bold{v}|| >0 \implies \lambda > 0$ .

Also, by putting the basis vectors instead of $\bold{v}$ , we get that the diagonal entries must also be positive.

Although positive definite matrices don’t have to be symmetric, a lot of texts put the restriction in the definition itself. And I’m going to do the same. So when I say “positive definite”, I actually mean “symmetric positive definite”. Am I being a little bitch here ? Absolutely ! But you’ll just have to deal with it :)

Symmetric matrices

Any matrix which is equal to its transpose is symmetric.

Spectral theorem : if $\bold{A}$ is a symmetric matrix, then the eigenvectors can be orthonormal and span the whole column space of $\bold{A}$ .

Proof of orthogonality : Suppose $\bold{v_1,v_2}$ are eigenvectotrs with unequal eigenvalues $\lambda_1,\lambda_2$ , then $\bold{v_1^TA^T}=(\bold{Av_1})^T = \lambda_1\bold{v_1}^T \implies \bold{v_1^TA^Tv_2} = \lambda_1\bold{v_1^Tv_2}$ . But $\bold{A^T=A}$ . Thus, $\bold{\lambda_1 v_1^Tv_2 = v_1^TAv_2 =v_1^T(\lambda_2v_2)}$ . But since $\lambda_1 \neq \lambda_2$ , so we have $\bold{v_1^Tv_2=0}$ and thus $\bold{v_1,v_2}$ are perpendicular if they have unequal eigenvalues. In other words, any two eigenvectors from eigenspaces of different eigenvalues are orthogonal. And we already know, that the eigenvectors in the same eigenspace can be chosen such that they are orthogonal. Thus we can create an orthonormal basis using all the eigenvectors.

The other fact that these eigenvectors span the column space is hard to prove. This fact allows us to write $\bold{A = RDR^T=\sum \lambda_i v_iv_i^T}$ where $\bold{D,R}$ are a diagonal matrix and an orthogonal matrix (rectangular or not), and $\bold{v_i},\lambda_i$ are the eigenvectors and corresponding eigenvalues for any symmetric matrix $\bold{A}$ . If $\bold{A}$ is not symmetric , then $\bold{R}$ is not an orthogonal matrix, but still has the linearly independent eigenvectors of $\bold{A}$ as its column vectors, and the equation is still correct. This is called eigenvalue decomposition.

Producing symmetric positive semidefinite matrices

For any matrix $\bold{M}$ (rectangular, singular, anything..), the matrix $\bold{M^TM}$ is symmetric positive semi-definite because 1) ..$\bold{(M^TM)^T = M^TM}$ and 2) ….$\bold{x^TM^TMx=(Mx)^T(Mx)=||Mx||^2}\geq 0$ . If the matrix is also non-singular, then the last inequality becomes strict and our composed matrix becomes symmetric definite.

Now you might wonder if the reverse can also be done ? That is, get a matrix $\bold{M}$ , given the matrix $\bold{M^TM}$ . It is certainly possible and can be done by the Cholesky Factorization

Cholesky Factorization

Given a symmetric matrix $\bold{A}$ with rank $n$ , we can write $\bold{A=LL^T}$ where $\bold{L}$ is an upper triangular matrix with $n$ rows and positive diagonal entries. On paper, this would look like this :

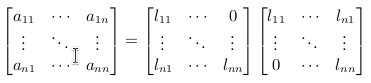
The first column vector on the RHS has the elements $l_{11}^2,l_{11}l_{21},\dots l_{11}l_{n1}$ and thus first gives the value of $l_{11}$ and then all of $l_{i1}$. Now that you know the first column, you can easily form the equations for $l_{22}l_{i2}$ . Again, get $l_{22}$ first and then get all the other values. Keep repeating this procedure and you’ll end up knowing all columns of $\bold{L}^T$ .

Singular Value decomposition

For any matrix $\bold{A}$ , we can write $\bold{A=U\Sigma V^T} = \sum\bold{\sigma_iu_iv_i^T}$ where $\bold{U,V}$ are orthogonal square (rotation) matrices with unit column vectors $\bold{u_i,v_i}$ and $\bold{\Sigma}$ is a diagonal matrix (with 0 padding where necessary) with entries $\sigma_i$ . On paper it looks like this :

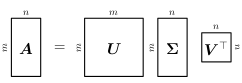
We can get $\bold{U,V}$ by eliminating the other matrix like this :

and then performing eigenvalue decomposition of the matrices on LHS and assigning values to matrices. Note that the shape of $\bold{\Sigma^2}$ is possibly different in both equations. this is accounted for by some entries in the bigger version being 0.

Notice that although it looks like it, $\bold{\Sigma}$ is not the diagonal matrix obtained on eigenvalue decomposition of $\bold{A}$ . But it can be if $\bold{U=V}$ , since then the equation on the top is basicaly the eigenvalue decomposition. In that case, we have $\bold{AA^T=A^TA=\Sigma^2}$ . This is a neccesary and sufficient condition for $\bold{A}$ to be diagonalisable, or “normal” . In the other case, we say that $\bold{A}$ is “deficient”.

The summation form in the topmost equation can be used to approximate the matrix $\bold{A}$ as a sum of lower rank matrices. this is used in image compression. It’s also the value of the spectral norm of the matrix, which is the maximum scaling a vector receives when passed through the matrix. Basically, the spectral norm is :

$||\bold{A}||_2 = \max_\bold{x}(\bold{\large\frac{||Ax||_2}{||x||_2}}) = \max_i \sigma_i$

The last equality is can be proved like this : $\bold{||Ax||^2=x^TA^TAx=\sum_ix^T(u_i\sigma_i^2u_i^T)x=\sum_i\sigma_i^2(u_i^Tx)^2 \leq \sigma_\text{max}^2\sum(u_i^Tx)^2=\sigma_\text{max}^2||x||^2}$ The last equality is because $\bold{U}$ is orthogonal

Eckart-Young theorem

Consider a rank-$r$ matrix $\bold{A}\in \mathbb{R}^{m\times n}$ with the singular value decomposition $\bold{A=U\Sigma V^T}=\sum_{i=1}^r\sigma_i\bold{u_iv_i^T}$ and the rank-$k$ approximation . For any rank-$k$ matrix $\bold{B}\in\mathbb{R}^{m\times n}$ with $k\leq r$, we have $\bold{||A-B||_2}\geq\sigma_{k+1}$, where equality happens when $\bold{B}=\sum_{i=1}^k\sigma_i\bold{u_iv_i^T}$ .

Proof : Since $\bold{B}$ has rank $k<r$ , we can construct a vector $\bold{w}$ that lives in the null space of $\bold{B}$ using the first $(k+1)$ columns of $\bold{V}$ . Suppose $\bold{w=\alpha_1v_1+\alpha_2v_2 + \dots+\alpha_{k+1}v_{k+1}} = \bold{V_ka}$ where $\bold{V_{k+1}}$ is the matrix with $\bold{v_i}$ as column vectors and $\bold{a}$ is the column vector with entries $\alpha_i$ . Also, suppose that the $k$ linearly independent column vectors as stacked up as row vectors to form $\bold{Y}^T$ , then the matrix $\bold{Y^TV_k}$ has shape $k\times (k+1)$ and thus the equation $\bold{Y^TV_ka=0}$ is solvable (because you can just do Gaussian elimination with some columns not being 0. Then find the specific solution by setting the coordinates in $\bold{a}$ to 0 for such columns). Thus there is a vector $\bold{w =V_ka}$ that is orthogonal to all the $k$ linearly independent vectors in $\bold{B}$ and is thus in the null space of $\bold{B}$ .

The first inequality is due to the definition of spectral.

Mind Map

Yes, yes.. this isn’t my style, and neither is it yours, but since it’s given to us just like that, we might as well ..