Models as Graphs

Every node is a random variable and every edge shows a dependency, which combined for a certain node can be expressed as probability distribution functions.

For example, in a graph like this :

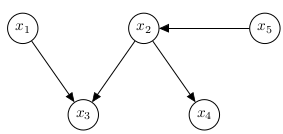
Since in the graph $x_3$ depends only on $x_1,x_2$ , we have a way to determine the distribution $p(x_3|x_1,x_2)$ without requiring to know the values or probability distributions of any other variables . If we know the probability distribution for the nodes that don’t have any arrows pointing in, then we basically know the actual (not conditional) probability distribution of every variable. These “grandparent” nodes’ distribution is usually either assumed , or approximated empirically.

Bayesian update

Notice that when some of the random variables are known, we can directly update the probability distributions of the children nodes and their children, and so on. But we can also update the parent nodes via Baeysian inference, and thus, also the sibling nodes. What we can’t (or don’t need to) update are the “co-parent” nodes, that is nodes that are also parents of the children of our known nodes. For example it graph above, if $x_2$ is known, then we know the pdf of $x_4$ and we can update the pdf of $x_5$ . We now also know the pdf of $x_3$ , but we have used the old pdf of $x_1$ to figure it out. That old pdf of $x_1$ has not changed, because althought the pdf of $x_3$ was altered, we did so using our prior beliefs about $x_1$ and using Baeysian inference again to update the pdf of $x_1$ will do nothing but echo that belief.

Conditionally independent nodes

Nodes $a,b$ that are independent, provided the values of some other nodes $c_1,c_2,\dots$ , are said to be conditionally independent under the set of nodes $C = \{c_1,c_2,\dots\}$. We write this as $(a\perp b \;|c_1,c_2,\dots)$ . A way to determine this is by forgetting that $c_i$ are random variables and seeing them as arbatory constants in the distribution functions of their parent nodes, and thus enabling us to delete these nodes completely . Now, in this scenario, if $a,b$ have to be independent, then there should be no effect of node $a$ on $b$ , directly, or indirectly. That happens when for every path that goes from $a$ to $b$ , in the original graph, there is some roadblock after deletion of nodes, either because the path contained a node from $C$, and now it’s incomplete (note that such a node shouldn’t have both the arrows connected to it in the path, pointing towards it, because then, this node, while being deleted would have formed a connection between its parent nodes and thus information can still be transmitted through this “broken” path), or because it contains a node, not in $C$ with the arrows attached to it from the path, both pointing in, making $a$ and $b$ the grandparent nodes. We know that knowing one grandparent node doesn’t cause us to update our beliefs about the other.